Nicht-einzigartige Elemente in Javascript finden

Es ist ein bisschen verwunderlich, dass Algorithmen quasi überall sind – und die Entwickler heutzutage von ihrer Existenz meist dennoch gänzlich unberührt und unbeeindruckt bleiben. Auch ich war die längste Zeit der Meinung, dass tiefergehendes Wissen über Algorithmen nur für Developerteams relevant ist, die sich mit Programmiersprachen und der Entwicklung von Framework Cores beschäftigen.

— Wen interessiert schon, wie Array.sort() genau funktioniert? Hauptsache es tut seinen Job und tut ihn schnell genug, oder?

Mit genau dieser Einstellung machte ich mich letztes Jahr auf den Weg zum Facebook Hacker Cup – zumindest ein T-Shirt wollte ich dort gewinnen. Gescheitert bin ich dann gleich in der ersten Runde. Ich war enttäuscht und begann, mir ernsthaft Gedanken darüberzumachen, wie ich mich verbessern könnte. Basierend auf diesen Überlegungen bin ich dann irgendwann zaghaft in die verwirrende, aber gleichermaßen faszinierende Welt der Algorithmen eingetaucht.

Damit dieser Erfahrungsbericht hier nicht ins Unendliche ausufert, denken wir am besten gemeinsam ein kurzes Beispiel durch.

Die Aufgabenstellung lautet wie folgt:

Wir haben in einem Datenfeld eine Folge ganzer Zahlen und möchten alle nicht-einzigartigen Elemente darin finden.

Die Naive Lösung

Am besten denken jetzt alle interessierten Leser selbst kurz darüber nach, wie sie dieses Problem in Angriff nehmen würden. Meine erste funktionierende Lösung war jedenfalls diese:

var length = data.length;
var unique = [];
var distinct = [];
for (var i = 0; i < length; i++) {
    var elem = data[i];
    var uniqueInd = unique.indexOf(elem);
    if (uniqueInd > -1) {
        unique.splice(uniqueInd, 1);
    }
    if (distinct.indexOf(elem) === -1) {
        distinct.push(elem);
        unique.push(elem);
    }
}
for (var i = length - 1; i > -1; i--) {
    if (unique.indexOf(data[i]) > -1) {
        data.splice(i, 1);
    }
}
return data;

Zu jener Zeit, als ich diesen Code geschrieben habe, hatte ich keine Ahnung von funktionellen Javascrip-Methoden, wie z.B. map oder reduce. Kein Wunder, dass diese erste Lösung ziemlich lang geworden ist. Nichtsdestotrotz: Sie brachte das gewünschte Ergebnis und ich war ganz schön stolz auf mich selbst. Weniger als einen Tag habe ich dafür gebraucht.

Dann beschloss ich, meinen Ansatz auf https://js.checkio.org/mission/non-unique-elements/ zu posten, um meine Idee mit anderen Lösungen zu vergleichen.

Die nett anzusehende Lösung

Sobald man seinen eigenen Code auf dieser Webseite veröffentlicht hat, bekommt man Zugang zu den Lösungsansätzen anderer Entwickler.

Und ganz oben in der Liste war diese Schönheit:

return data.filter(function(a){
    return data.indexOf(a) !== data.lastIndexOf(a)
});

Der Code ist kurz, lesbar und elegant. Die Idee dahinter genauso simpel wie brillant: Wenn das erste und letzte Vorkommen eines Elements ein- und dasselbe ist, existiert dieses Element nur einmal, es ist also einzigartig.

Sehen Sie sich nur diesen Ansatz an und vergleichen Sie ihn mit meiner Idee. Da liegen Welten dazwischen, richtig?

Ich war beeindruckt und mein Ehrgeiz war angestachelt, daher begann ich, an anderen Programmier-Wettbewerben teilzunehmen. Einer davon brachte mich schließlich auf die Landau-Symbole (im englischsprachigen Raum meist als Notation bezeichnet).

Die Schnelle Lösung

Um schnell zu erkennen, warum die Landau-Symbole hier Sinn machen, sollten wir uns folgende Tabelle aus einem Buch von „Steven Skiena“ ansehen.

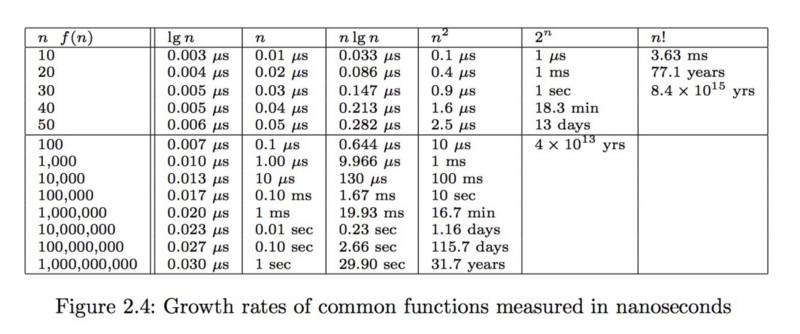
Nehmen wir an, unser Algorithmus hat eine Komplexität von . Das bedeutet, dass es ungefähr 16,7 Minuten dauern wird, um ein Datenfeld mit 1 Million Zahlen zu bearbeiten. Ein bisschen viel, finden Sie nicht? Wenn man bedenkt, dass die Teilnehmer des Facebook Hacker Cups nach Erhalt der Input-Daten nur fünf Minuten Zeit haben, um Ergebnisse hochzuladen, ist das auf jeden Fall zu viel.

Sieht unsere nett anzusehende Lösung also immer noch so nett aus, wenn wir sie vom Standpunkt der Algorithmus-Komplexität betrachten? Ähnlich wie bei meiner ersten Lösung lautet die Antwortet „Leider Nein“. Und zwar darum:

indexOf und lastIndexOf nutzen im schlimmsten Fall (wenn wir eine Folge ausschließlich einzigartiger Zahlen haben) Rechengänge, da sie im Grunde genommen konstant und wiederholt die gesamten Daten durchgehen. Da wir dies innerhalb der filter-Methode ausführen, bei der es sich um eine Schleife handelt, bedeutet das, dass wir Rechengänge Mal ausführen, was wiederum ergibt. Oops. Das ist unzumutbar langsam.

Eine Methode, um diese Schwachstelle zu korrigieren, ist der Einsatz einer Sortierung. In den Grundlagen der Wissenschaft der Algorithmen wird uns gelehrt, dass wir mit einer Komplexität sortieren können, was laut der obenstehenden Tabelle wesentlich schneller vonstattengeht als und sogar bei einer Menge von einer Million Datensätze in einem vernünftigen Zeitraum fertiggestellt werden kann.

Sobald wir die Liste sortiert haben, können wir uns einen weiteren Trick aus dem Einmaleins der Algorithmen zunutze machen, indem wir die indexOf und lastIndexOf –Methoden mit einer Binärsuche überschreiben. Die grundlegende Idee hinter der Binärsuche ist, dass wir die durchsuchbare Reihe bei jedem Schritt in zwei Teile aufbrechen und ab da nur in einer davon weitersuchen. Dabei überprüfen wir einfach nur, ob die Zahl in der Mitte der Reihe größer oder kleiner ist als jene, nach der wir gesucht haben. Dann wählen wir abhängig von der Sortierung den linken oder den rechten Teil. Und zwar so lange, bis wir eine Reihe mit nur einem Element vorliegen haben – bei dem es sich entweder um das eine Element handelt, nach dem wir gesucht haben, oder eben nicht, was bedeuten würde, dass unser Element gar nicht in der Reihe enthalten ist. Um diesen Vorgang zu vollenden, benötigen wir x Schritte, wobei = (da wir unsere Datenmenge bei jeder Iteration durch 2 teilen), wodurch wir eine Komplexität von erhalten, um sowohl indexOf, als auch lastIndexOf finden zu können. Und da haben wir für die Methodenaufrufe indexOf und lastIndexOf insgesamt eine Komplexität von .

Zu guter Letzt haben wir innerhalb jeder Iteration (da wir mit filter eine Iteration durch die gesamte Reihe durchführen) eine Schleife von mit einer Komplexität wodurch wir als gesamte Komplexität erhalten.

Dies verhält sich genauso wie die vorher beschriebene Sortierung, weshalb wir schlussendlich für den gesamten Algorithmus erhalten. Cool! Das ist wesentlich schneller.

Jetzt können wir sogar eine Milliarde Datensätze in weniger als einer Minute bewältigen.

Und so können wir indexOf mit einer Komplexität in einer sortierten Reihe anwenden:

function newIndexOf(array, elem, startIndex, endIndex) {
    if (array.length === 1) {
        if (array[1] === elem) {
            return startIndex;
        } else {
            return -1;
        }
    }
  
    var median = Math.floor(array.length / 2);
  
    if (elem <= array[median]) {
        return newIndexOf(array, elem, startIndex, median);
    } else {
        return newIndexOf(array, elem, median + 1, endIndex);
    }
}

Die Implementierung von lastIndexOf wird dieselbe sein, allerdings nutzen wir anstatt der Bedingung „≤”, die Bedingung „<”.

Die noch schnellere Lösung

Aber wenn wir es mit einem Webserver mit einer hohen Serverbelastung zu tun haben, sind sogar 30 Sekunden noch viel zu viel. Können wir das noch schneller machen?

Ja! Jedes Mal, wenn ich über Advanced Array Utilities (also Tools zur Bearbeitung von Datenfeldern) nachdenke, komme ich auf die lodash.js Library. Und so lautet deren Vorschlag in dieser Sache:

_.transform(_.countBy(array), function(result, count, value) {
    if (count > 1) result.push(value);
}, []);

Zuerst nutzen wir die countBy-Methode, um das Vorkommen eines jeden Elements zu berechnen. So erhalten wir ein JS-Object, das Elemente als Schlüssel und deren Vorkommen als Werte aufweist. Die countBy-Methode nützt die JS reduce-Methode und übernimmt eine Zeitkomplexität, da es quasi einmal das gesamte Datenfeld durchläuft.

Dann gehen wir mit transform durch alle Schlüssel, die wir im Objekt haben und nehmen all jene, die einen Wert (also ein Vorkommen) von größer als 1 haben, wodurch wir ebenfalls wieder die Komplexität erhalten, da wir nicht mehr als Schlüssel in diesem Objekt haben können.

Und da haben wir eine Komplexität von als Endresultat. Wenn wir nun einen hoffnungsfrohen Blick auf die Tabelle oben werfen, werden wir erfreut feststellen können, dass wir nun eine Milliarde Datensätze 30 Mal schneller bearbeiten können. Wow!

Das Fazit

In meiner kurzen Analyse konnten wir bestätigen, dass sich Frameworks und Utility Bibliotheken wie lodash.js für gewöhnlich perfekt um die Zeitkomplexität von Algorithmen kümmern und wir ihnen diesbezüglich vertrauen können.

Gleichzeitig besteht immer die Gefahr, dass wir uns von nett anzusehendem und clever aussehendem Code blenden lassen, der die Performance unserer App im Endeffekt allerdings deutlich bremsen wird.

Obwohl es daher kaum empfehlenswert ist, komplexe Algorithmen selbst zu erstellen, schadet es nicht, wenn wir zumindest in der Theorie verstanden haben, wie die Komplexität eines bestimmten Algorithmus berechnet wird – denn so können wir sicherstellen, dass wir keine bösen Überraschungen erleben, sobald wir später entscheiden, unsere App auf größere Volumen zu skalieren.

Alle, die diesen Artikel wirklich spannend fanden und noch tiefer in diese Welt eindringen möchten, kann ich die Kurse und Lernbücher von Steven Skiena wärmstens ans Herz legen. Auf den Plattformen https://js.checkio.org/ und https://www.codewars.com/ kann man sich dann nach anfänglicher Lektüre selbst mit Code austoben und mehr Übung bekommen. Und wer weiß: Vielleicht begegnet man sich ja schon bald beim nächsten Programmier-Wettbewerb? 😉